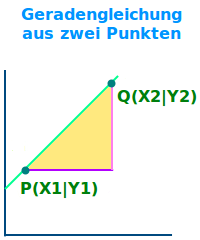
Geradengleichung aus zwei Punkten
y = 4x+1 rechnerisch aufstellen | Aufgaben unter => qck
Was wird erklärt?
◦ Man hat zwei Punkte von einer Geraden gegeben.
◦ Daraus soll eine Geradengleichung y=mx+b erstellt werden.
◦ Es wird erklärt, wie das geht.
Was wird nicht erklärt?
◦ Andere Methoden, zu Aufstellen einer Geradengleichung
◦ Dazu siehe unter => Geradengleichung aufstellen
Vorab
◦ P(2|4) meint einen Punkt in einem Koordinatensystem.
◦ P ist der Name des Punktes, man sagt oft "Punkt P".
◦ Links steht der x-Wert.
◦ Rechts steht der y-Wert.
Gegeben
◦ Punkt P(2|4)
◦ Punkt Q(10|24)
Gesucht
◦ Gleichung in Normalform y=mx+b
◦ b ist der => y-Achsenabschnitt
◦ m ist die => Steigung
Hinschreiben
◦ x-Wert vom ersten Punkt: X1=2
◦ y-Wert vom ersten Punkt: Y1=4
◦ x-Wert vom zweiten Punkt: X2=10
◦ y-Wert vom zweiten Punkt: Y2=24
Steigung m berechnen
◦ m=(Y2-Y1)/(X2-X1)
◦ m=(24-4):(10-2)
◦ m=20/8=2,5
Steigung m in Normalform einsetzen:
◦ y=2,5·x+b
◦ Jetzt noch einen der beiden Punkte einsetzen:
◦ Zum Beispiel Punkt P mit x=2 und y=4:
◦ 4=2,5·2+b
Umstellen nach b:
◦ 4=2,5·2+b | vereinfachen
◦ 4=5+b | -5
◦ b=-1
m und b in Normalform einsetzen:
◦ y=2,5x-1
◦ Fertig
Tipp
◦ Das x und y schreibt man am Ende immer als Variable.
◦ Statt y wird oft auch f(x) geschrieben.
Siehe auch
=> Geradengleichung aus Graph über zwei Punkte [Graphisch]
=> Zwei-Punkte-Form der Geradengleichung [Alternative]
=> Lineare Funktion [Übersicht]
=> qck
=> pdf
