Gerade zeichnen aus Steigung und y-Achsenabschnitt
Anleitung
Basiswissen
Man kennt die Steigung einer Geraden, das heißt einer linearen Funktion. Zusätlich kennt man noch den y-Achsenabschnitt. Hier steht eine ausführliche Anleitung, wie man daraus den Graphen zeichnet.
Was meint das?
- Gerade meint hier dasselbe wie der Graph einer linearen Funktion.
- Man soll eine Gerade in einem x-y-Koordinatensystem zeichnen.
- Die x-Achse ist die waagrechte Achse von links nach rechts.
- Die y-Achse ist die senkrechte Achse von oben nach unten.
Was meint y-Achsenabschnitt?
- Das ist der y-Wert, bei dem die Gerade durch die y-Achse geht.
- Der y-Achsenabschnitt ist immer das b in der Gleichung y=mx+b.
- Der y-Achsenabschnitt in unserem Beispiel ist 1.
Was meint Steigung?
- Die Steigung sagt einem, wie steil die Gerade bergauf geht.
- Dabei betrachtet man die Gerade immer von links nach rechts.
- Ist die Steigung negativ, dann geht die Gerade bergab.
- Die Steigung ist immer das m in der Gleichung y=mx+b.
- Die Steigung in unserem Beispiel ist 0,5.
Wie zeichnet man daraus den Graphen?
- Man fängt immer mit dem y-Achsenabschnitt b an.
- Nehmen wir an, wir hätten einen y-Achsenabschnitt von b=1.
- Dann markiert man auf der y-Achse bei 1 einen Punkt P.
- Der Punkt P liegt dann auf jeden Fall auf der Geraden.
Was fängt man mit der Steigung m an?
- Man geht jetzt wieder auf den Punkt vom y-Achsenabschnitt.
- Dann geht man von dort aus irgendeine Strecke waagrecht nach rechts.
- Gut sind Zahlen, die man leicht mit dem Wert der Steigung malnehmen kann, z. B. 6.
- So viele Kästchen oder Zentimeter geht man also vom y-Achsenabschnitt aus nach rechts.
- Man markiert den Punkt, an dem man dann angekommen bist, schreibe Q daran.
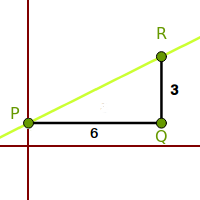
- Zur Kontrolle: unser Punkte Q liegt bei (6|1).
- Jetzt nimmt man den Zahlenwert der Steigung m.
- Die Steigung m könnte zum Beispiel 0,5 sein.
- Man rechnet dann die waagrecht gegangene Strecke mal der Steigung.
- Wenn man also 6 Kästchen nach rechts gegangen ist, kämen jetzt 3 Kästchen heraus.
- Gehe zum vorher markierten Punkt Q und von dort aus so viele Kästchen nach oben wie gerade berechnet.
- Achtung: wenn die Steigung negativ ist, dann muss man so viele Kästchen nach unten gehen.
- Dort markiert man wieder einen Punkt. Wir nennen ihn hier R.
- Zur Kontrolle: unser R im Beispiel liegt bei (6|4).
Die fertige Gerade
- Jetzt verbindet man den y-Achsenabschnitt bei P mit dem Punkt R.
- Diese Verbindungsstrecke ist die gesuchte Gerade.
Tipps
- Je weiter man vom y-Achsenabschnitt aus nach rechts geht, desto genauer wird die Gerade.
- Bei großen Steigung kann man aber nicht so weit nach rechts gehen, dann nimmt man z. B. ein Kästchen.