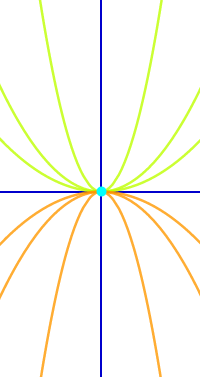
Gemeinsamen Punkt einer Kurvenschar berechnen
Anleitung
Basiswissen
Man hat eine Kurvenschar gegeben. Die Schar besteht aus theoretisch unendlich vielen Graphen. Manchmal, aber nicht immer, gehen alle Graphe einer Schar durch einen gemeinsamen Punkt. Hier steht, wie man diesen gemeinsamen Punkt berechnet (wenn es ihn gibt).
Verfahren
- Der Scharparameter sei hier a genannt.
- Ein gemeinsamer Punkt muss für unterschiedliche Parameterwerte gelten.
- Das heißt, zum Beispiel für a=3 und a=4 muss es einen Punkt mit gleichem x- und y-Wert geben.
- Das formuliert man mathematisch allgemein so:
- f(x) mit Parameter a muss gleich f(x) mit Parameter b sein.
- Man setzt die zwei Funktionsterme dann gleich.
- Durch die Gleichsetzung entsteht eine Gleichung mit a, b und x aber ohne y.
- Man löst diese Gleichung nach x auf. Dabei kann man a und b eliminieren.
- Eliminieren meint hier: es gibt eine Umformung durch die a und b verschwinden.
- Beispiel: x(2a-2b)=0
- Wenn - wie gefordert - a und b unterschiedlich sind, dann ...
- ist der Klammerterm immer auch ungleich 0.
- Man darf dann also auf beiden Seiten durch den Klammerterm teilen.
- Genau durch diese Äquivalenzumformung verschwinden mit der Klammer a und b.
- Verschwinden a und b, dann gibt es einen gemeinsamen Punkt, ansonsten nicht.
- Den Term für den x-Wert setzt man in f(x) mit beliebig gewähltem Parameterwert ein.
- Das ist der y-Wert.
Beispiele
- Betrachtet werden soll die Funktionsschar f(x)=ax².
- Parameter a und b unterscheiden und gleichsetzen gibt:
- ax²=bx²| jetzt Gleichung in Normfalform bringen:
- ax²-bx²=0 | jetzt x² ausklammern, also faktorisieren:
- x²(a-b)=0 | jetzt Satz vom Nullprodukt anwenden:
- Gleichung geht auf, wenn x=0 ist oder a und b gleich sind.
- Dass a und b gleich sind, wurde am Anfang verboten.
- Die zweite Lösung der Gleichung wäre, dass x=0 ist.
- Das ist also der x-Wert des gemeinsamen Punktes.
- Einsetzen in f(x) liefert den y-Wert: 0
- Also ist der gemeinsame Punkt: (0|0)