Funktion

f(x)

Basiswissen

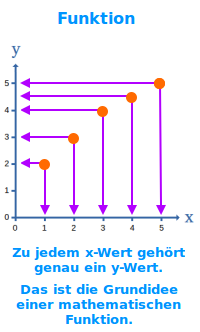
f(x)=4x+8 ist eine typische mathematische Funktion: man kann für x eine beliebige Zahl einsetzen. Die Rechnung gibt dann einen y-Wert als Ergebnis der eindeutig dem eingesetzten x-Wert zugeordnet ist. Das ist die Grundidee einer Funktion. Der Gedanke wird hier ausführlich erklärt.

Allgemeine Schreibweise von Funktionen

"Wenn x und y zwei variable (veränderliche) Größen sind und wenn sich einem gegebenen x-Wert genau ein y-Wert zuordnen lässt, dann nennt man y eine Funktion von x und schreibt: y = f(x)"^[1]. Mehr zu dieser Schreibweise steht im Artikel f(x) ↗

Definition von Funktion über x und y

Die allgemeine Definition einer Funktion lautet: "Unter einer Funktion versteht man eine Vorschrift, die jedem Element x aus einer Menge D genau ein y aus einer Menge W zuordnet. Symbolische Schreibweise: y = f(x) mit x ∈ D."^[4]

Definition von Funktion über Quellmenge- und Zielmenge

Eine Funktion ordnet jedem Element der Quellmenge (Definitionsmenge) genau ein Element der Zielmenge (Wertemenge) zu. Diese Elemente können Namen von Menschen, Farben, Körpergrößen, Gehälter oder psychologische Typen sein. In dieser allgemeinen Definition ist der Begriff der Funktion identisch mit dem mengentheoretischen Begriff der Abbildung. In der Schulmathematik beschränkt sich der Begriff der Funktion meist auf Mengen mit Zahlen. Siehe auch den allgemeinen Begriff der Abbildung ↗

Konkretes Praxisbeispiel einer Funktion

Man stelle sich ein tiefes Meer mit klarem Wasser vor. Man taucht gedanklich von oben nach unten ab. Die Tauchtiefe soll x sein. Man kann dann für jede Tiefe x genau einen Wert y für die Helligkeit angeben. Die Helligkeit ist damit eine Funktion der Tauchtiefe, kurz: Helligkeit = f(Tauchtiefe). Weitere Beispiele unter Funktionen nach Sachthemen ↗

Was ist eine Funktion in der Schulmathematik?

In der Schulmathematik ist eine Funktion meistens eine Gleichung.

Links steht ein f(x) oder ein y und rechts ein Funktionsterm.

Man kann rechts für x irgendeine beliebige Zahl einsetzen.

Damit rechnet man die rechte Seite aus.

Das Ergebnis ist dann f(x) oder y.

Die Gleichung ordnet jedem x-Wert ...

dadurch genau einen y-Wert zu.

Was ist das Besondere an einer Funktion?

Das Besondere ist, dass zu jedem x-Wert immer genau ein y-Wert passt.

Zu jeder x-Zahl, die man in die Funktionsgleichung einsetzt ...

passt immer genau eine y-Zahl, dass die Gleichung aufgeht.

Beispiel für eine mathematische Funktion

Wir nehmen die Gleichung: f(x)=4x+1

Man könnte auch schreiben: y=4x+1

Man kann jetzt gedanklich irgendeine Zahl für x einsetzen.

Wir nehmen die Zahl 100. Dann kommt auf der rechten Seite 401 heraus.

Welche Zahl muss man für y einsetzen, dass die Gleichung aufgeht?

Es passt nur die Zahl 401.

Also passt für x=100 nur y=401.

Das nennt man eine eindeutige Zuordnung:

Zu dem x-Wert passt genau eindeutig ein y-Wert.

Und genau so etwas nennt man eine Funktion.

Gegenbeispiele: keine Funktion

Wir nehmen die Gleichung y²=x.

Man kann wieder für x irgendeine Zahl einsetzen.

Wir nehmen die Zahl 4.

Welche y-Werte würden passen, dass die Gleichung aufgeht?

Man kann für y zum Beispiel die 2 einsetzen: denn 2·2 gibt 4.

Man kann aber auch die -2 einsetzen, denn: -2·(-2) gibt auch 4.

Jetzt passen zu einem x-Wert plötzlich 2 y-Werte.

Und das ist für eine Funktion nicht erlaubt.

y²=x ist also keine eindeutige Zuordnung.

Es ist eine mehrdeutige Zuordnung.

Was meint das f(x)?

In Schulbüchern wird manchmal das f(x) und manchmal das y geschrieben.

Man benutzt das f(x) gerne, um damit zu zeigen, dass es um eine Funktion geht.

Wenn man liest: f(x)=x²-2, dann weiß man: das ist wirklich eine Funktion.

Wenn man liest: y=x²-2, dann kann es - muss aber keine - Funktion sein.

Wie erkennt man Funktionen an Graphen?

Die x-Achse muss von links nach rechts gehen.

Die y-Achse muss von unten nach oben gehen.

Wenn das so ist, dann funktioniert immer die folgende Methode:

Man überprüft, ob der Graph irgendwo zwei oder mehr Punkte ...

senkrecht übereinander hat. Wenn ja, gehört er nicht zu einer Funktion.

Ansonsten schon.

Gibt es auch Funktionen ohne Zahlen?

Ja, man kann zu Beispiel jeder Frucht immer genau eine Farbe zuordnen und das in einer Tabelle darstellen. Die Zuordnung wäre dann eine Funktion. Oder man ordnet jedem Bereich im Gehirn eine psychische Funktion zu. Auch das wäre eine Funktion. Diese Art von zahlenlosen Funktionen kommen zum Beispiel in der Informatik häufig vor.

Was ist die Funktionentheorie?

Als Funktionentheorie bezeichnet man ein Gebiet der höheren Mathematik, wie es an Hochschulen unterrichtet wird. Dabei geht es um Auf- und Ableitungen von sogenannten komplexen Zahlen. Komplex nennt man Zahlen, die auch abseits von der Zahlengeraden liegen können. Siehe mehr dazu im Artikel Funktionentheorie ↗

Funktionen in der Physik

Für viele Physiker gilt die Vorhersagbarkeit von Abläufen in der Wirklichkeit als bestmögliches Ziel ihrer Arbeit^[5]. Wenn man zu Beispiel eine Theorie hat, die immer eindeutig und zuverlässig vorhersagen kann, wie lange ein fallender Stein benötigt, um aus einer bestimmten Höhe bis auf den Boden zu fallen, dann gilt die Theorie als brauchbar, wahr oder gut. Wenn etwas aber praktisch eindeutig vorhersagbar ist, dann kann man auch eine Tabelle aufstellen mit der Ausgangssituationen und der dazugehörigen Endsituationen. Damit heißt praktische Vorhersagbarkeit immer auch, dass man dafür eine Funktion angeben kann. Dass man dafür Gleichungen verwendet ist nicht zwingend nötig, aber praktisch. Die Gleichungen enthalten meist sozusagen eine unendlich große Anzahl möglicher Vorhersagen, die man aber oft mit minimalem Aufwand aufschreiben kann. Ob aber wirklich alle Vorgänge in der Physik vorhersagbar sind, ist eine offene Frage. Siehe auch Vorhersagbarkeit ↗

Fußnoten

[1] Guido Walz: Spektrum Lexikon der Mathematik. Band 2: Eig bis Inn; 2001; ISBN: 3-8274-0437-7: Funktion ist synonym mit Abbildung, aber oft eingeschränkt auf Zahlen

[2] Bronstein, Semendjajew, Musiol, Mühlig: Taschenbuch der Mathematik. 10. Auflage, 2016. ISBN: 978-3-8085-5789-1. Verlag Harri Deutsch. Seite 49.

[3] 1905. Funktion noch nicht als eindeutige Zuordnung: " Funktion bezeichnet in der Mathematik, aber auch sonst die Abhängigkeit einer Größe von einer oder von mehreren andern. So ist der Flächeninhalt eines Quadrats eine F. der Seite des Quadrats, der Widerstand, den ein aus einem Geschütz abgefeuertes Geschoß in der Luft findet, eine F. der Geschwindigkeit des Geschosses, die Geschwindigkeit, mit der das Geschoß die Mündung verläßt, eine F. der Pulverladung etc. Über den allgemeinen Begriff der F. einer und mehrerer Veränderlichen, über Eindeutigkeit, Stetigkeit und Differentiierbarkeit von Funktionen s. Differentialrechnung, S. 906. Ist y als F. von x bestimmt durch eine nach y aufgelöste Gleichung von der Form: y = f(x), so sagt man, y ist eine explizite F. von x, ist es durch eine Gleichung von der Form: F(x, y) = 0 bestimmt, z. B. durch die Gleichung x2+y2 = 1, aus der folgt: y = √(1-x2), so sagt man: y ist eine implizite F. von x. Ist y = f(x), so gehört nicht nur zu jedem Werte von x ein oder mehrere Werte von y, sondern auch umgekehrt zu jedem Werte von y ein oder mehrere Werte von x, es ist also auch x eine (implizite) F. von y, die man durch Auflösung der Gleichung y = f(x) nach x erhält. Ergibt sich etwa x = φ(y), so nennt man die beiden Funktionen f(x) und φ(y) zueinander invers oder sagt: die eine ist die Umkehrung der andern. So sind die Funktioneny = x/1+x und x = y/1-y, zueinander invers. Auf der Einführung der inversen F. beruht ferner das Wurzelausziehen und das Rechnen mit Logarithmen (s.d.), denn die zu y = xn inverse F. ist: x = n√y und die zu y = ax inverse ist: x = dem Logarithmus von y für die Basis a. Von großer Wichtigkeit sind die Funktionen von x, deren Argument x nicht bloß reelle, sondern auch komplexe Zahlenwerte annehmen kann, bei denen man also x = a+bi setzen kann, unter a und b beliebige reelle (positive oder negative) Zahlen und unter i die Quadratwurzel aus -1 verstanden: i = √-1. Die Lehre von diesen Funktionen einer komplexen Veränderlichen bildet den Hauptinhalt der modernen Funktionentheorie, die namentlich durch Cauchy, Riemann und Weierstraß geschaffen worden ist. Insbesondere verdankt man Weierstraß den Begriff und die Theorie der analytischen, d. h. der durch Potenzreihen (s.d.) darstellbaren Funktionen. Den ersten Anstoß zur Entwickelung einer solchen allgemeinen Funktionentheorie hat die Integralrechnung (s.d.) gegeben, die überhaupt die ergiebigste Quelle immer neuer Funktionen ist. Durch die Betrachtung gewisser Integrale wurden z. B. Abel und Jacobi auf die elliptischen Funktionen geführt, von denen die elementaren trigonometrischen Funktionen sin x, cos x etc. (s. Trigonometrie) und die Exponentialfunktion (s.d.) besondere Fälle sind. Indem anderseits Abel die Integrale beliebiger algebraischer Funktionen untersuchte, gelangte er zu einem äußerst allgemeinen Satz über diese Integrale, der unter dem Namen des Abelschen Theorems bekannt ist, und auf den gestützt Riemann und Weierstraß die Theorie einer nach allgemeinern Klasse von Funktionen, der sogen. Abelschen, ausbauten. Auch sonst hat man noch eine Menge von verschiedenen Funktionen untersucht und mit besondern Namen belegt, z. B. die Gammafunktion, die Thetafunktionen, die Modulfunktionen etc., und auch in Zukunft wird es von Zeit zu Zeit immer wieder nötig sein, neue Gattungen von Funktionen in die Analysis einzuführen, so daß da kein Ende abzusehen ist. – Den Ausdruck F. hat Leibniz zuerst in dem hier betrachteten Sinne gebraucht, doch verstanden er und seine Nachfolger, besonders Euler und Lagrange, unter einer F. von x nur einen gegebenen oder gegeben gedachten Rechenausdruck, der irgendwie aus x gebildet ist. Der allgemeine Begriff der F. (s. Differentialrechnung) stammt von Dirichlet, er ist aber in seiner Allgemeinheit zur Untersuchung nicht geeignet, wenn man nicht von vornherein die F. als stetig voraussetzt. Lange Zeit glaubte man beweisen zu können, daß eine stetige F. notwendig auch differentiierbar sei, bis es Weierstraß gelang, eine stetige F. zu bilden, die gleichwohl nicht differentiierbar ist. Vgl. Dini, Grundlagen für eine Theorie der Funktionen (a. d. Ital. von Lüroth u. Schepp, Leipz. 1892); Durège, Elemente der Theorie der F. einer komplexen veränderlichen Größe (4. Aufl., das. 1893); Thomae, Elementare Theorie der analytischen F. (2. Aufl., Halle 1898)." In: Meyers Großes Konversations-Lexikon, Band 7. Leipzig 1907, S. 212. Online: http://www.zeno.org/nid/20006643221

[4] 1911, Funktion als Abhängigkeit: "Funktion (lat.), Verrichtung (in einem bestimmten Wirkungskreis), Wirksamkeit. In der Mathematik heißt F. einer veränderlichen Größe eine von dieser abhängige Größe, die aus einem gegebenen Wert jener Veränderlichen berechenbar ist. Diese abhängige Größe kann aus einer oder mehrern Veränderlichen mit oder ohne Konstanten bestehen. Soll y eine F. der Veränderlichen x sein, so drückt man dies aus durch: y = f (x). – Funktionieren, in F. sein; Funktionär, Beamter." In: Brockhaus' Kleines Konversations-Lexikon, fünfte Auflage, Band 1. Leipzig 1911., S. 632. Online: http://www.zeno.org/nid/20001124684

[5] 1923, zur Geschichte des Funktionsbegriffes: "Wie functio zu der Bedeutung der quantitativen Abhängigkeit gekommen ist, das gehört in die Geschichte der Mathematik; es ist bekannt, daß functio bei den ersten Analytikern der Geometrie nur eine besonders ausgezeichnete Art der Abhängigkeit bezeichnete, die verschiedenen Potenzen der gleichen Zahl, so daß bei den einfachsten Aufgaben die Fläche des Quadrats und der Inhalt des Würfels als Funktionen einer Seite erschienen; die großen Mathematiker dehnten den Funktionsbegriff dann weiter aus, bis er in der zweiten Hälfte des 19. Jahrhunderts zu einer Grundlage werden konnte, auf der die Arithmetisierung aller mathematischen Disziplinen mit unerhörter Strenge aufgebaut werden konnte. Ich möchte aus diesen mir nur schwer zugänglichen Gebieten das Eine erwähnen, daß auch diese mathematische Abhängigkeit noch ein unbestimmter Ausdruck ist, weil die Formel y = f(x) auch dann gebraucht werden darf, wenn die Relation zwischen y und x nicht eindeutig bestimmt werden kann." Der gesamte Artikel in dem Lexikon aus dem Jahr 1923 ist sehr viel länger und geht breit auch auf philosophische Bedeutungen ein. In: Mauthner, Fritz: Wörterbuch der Philosophie. Leipzig 1923, Band 1, S. 525-532. Online: http://www.zeno.org/nid/20006180582

[4] Die allgemeine Definition einer Funktion lautet: "Unter einer Funktion versteht man eine Vorschrift, die jedem Element x aus einer Menge D genau ein y aus einer Menge W zuordnet. Symbolische Schreibweise: y = f(x) mit x ∈ D." In: Lothar Papula: Mathematik für Ingenieure und Naturwissenschaftler. Ein Lehr- und Arbeitsbuch für das Grundstudium. Band 1. 14. Auflage, 2019. ISBN: 978-3-658-05619-3. Verlag Springer Vieweg. Seite 146, dort das Kapitel III Funktioneen und Kurven. Siehe auch Der Papula ↗

[5] Die Vorhersage von Ergebnissen bei Experimenten als Ziel von Wissenschaft: "Die Prüfung jeden Wissens ist das Experiment. Das Experiment ist der einzige Richter wissenschaftlicher 'Wahrheit'." Im englischen Original: "The test of all knowledge is experiment. Experiment is the sole judge of scientific 'truth'." In: Feynman, R.P.; R.B. Leighton and M. Sands, 1963. The Feynman Lectures on Physics, Reading, MA: Addison-Wesley Publishing Company. Page 1-1. Siehe auch Vorhersagbarkeit ↗

zur Bildbeschreibung mit Autoren- und Urheberinfos — Eine Funktion als Graph: jeder Punkt zeigt auf einen x- und einen y-Wert. Der Punkt gibt für jeden x-Wert immer genau einen y-Wert an. Man sagt: die Funktion ordnet jedem x-Wert eindeutig einen y-Wert zu. Funktionen können - müssen aber nicht - als Graph dargestellt werden. Sie können - müssen aber nicht - Zahlen einander zuordnen. Gunter Heim