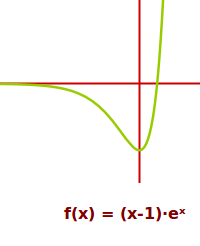Extrempunkte von Exponentialfunktionen
Gibt es nur unter besonderen Bedingungen | Beispiel
Basiswissen
Exponentialfunktionen sind Funktionen, bei denen das x im Exponenten einer Potenz vorkommt. Üblicherweise ist die Basis der Potenz eine konstante Zahl, etwa 2 oder auch die eulersche Zahl e. Reine Exponentialfunktionen haben keine Extrempunkte (und auch keine Wendepunkte). Werden sie aber verknüpft mit anderen Funktionen, können Extrempunkte (und auch Wendepunkte) daraus entstehen. Zur Definition siehe auch Exponentialfunktion ↗
Keine Extrempunkte
- Beispiel: f(x) = 4^x
- Hat keine Extrempunkte:
- Eine Exponentialfunktion an sich hat die die Form: f(x) = (Term ohne x) hoch (Term mit x)
- Der Graph einer solchen Funktion hat weder Hoch- noch Tiefpunkte, also keine Extrempunkte.
- Mehr dazu unter Exponentialkurve ↗
Mögliche Extrempunkte
- Beispiel: (x-1)·e^x
- Kann Extrempunkte haben:
- Man kann Exponentialfunktion rechnerich mit anderen Funktionen verbinden.
- Im Beispiel ist die lineare Funktion f(x)=x-1 verknüpft mit der e-Funktion e^x.
- Die Graphen solcher Verknüpften Funktionen können Hoch- und Tiefpunkte haben.
- Siehe auch veknüpfte Funktion (externer Link)
Berechnung
- Man geht formal vor wie bei allen Funktionen Extrempunkte bestimmen ↗
- Man leitet die Funktion f(x) ab zu f'(x):
- Man bestimmt die Nullstellen von f'(x).
- Das sind mögliche Extremstellen.
Besonderheiten
- Je nach Art der Verknüpfung braucht man aber spezielle Ableitungsregeln.
- Sind die Funktionen mit mal verknüpft, siehe unter Ableiten über Produktregel ↗
- Sind die Funktionen verkettet, siehe unter Ableiten über Kettenregel ↗
Beispiele
- Die folgenden Exponentialfunktionen haben je einen Extrempunkt:
- f(x) = (x-1)·e^x
- f(x) = a^2-x