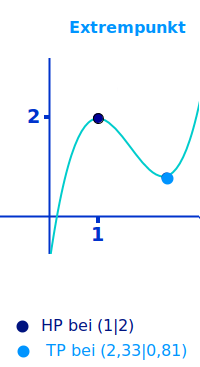
Extrempunkt
Definition
Basiswissen
Zu den Extrempunkten von Funktionen f(x) zählen nur Hoch- und Tiefpunkte. Man kann Extrempunkte über die erste Ableitung f'(x) und die zweite Ableitung f''(x) bestimmen. Aber mit der schulüblichen Definition der Extrempunkte ergeben sich zwei Probleme, die hier kurz besprochen (und gelöst) werden.
Was alle Extrempunkte gemeinsam haben
Ein Extrempunkt ist immer nur ein Hoch oder Tiefpunkt. Wende-, Sattel oder sonstige besonderen Punkte eines Graphen einer Funktion gehören nicht dazu. Allen Definitionen eines Extrempunktes ist gemeinsam, dass es zu einem Extrempunkt innerhalb eines betrachteten Intervalls keine höheren (Hochpunkt) oder tieferen (Tiefpunkt) Punkte gibt. Davon ausgehend gibt es unterschiedliche, leicht voneinander abweichende Definitionen.
Immer zusammen mit Intervall
Alle Definition von Extrempunkten gelten immer nur für ein bestimmtes Intervall, also von einem kleinsten x-Wert bis zu einem größten x-Wert. Ist kein Intervall angegeben, geht man üblicherweise vom gesamten Definitionsbereich (alle erlaubten x-Werte) einer Funktion aus. Ist ein Intervall angegeben, spielt es keine Rolle, wie sich die Funktion außerhalb des Intervalls verhält. Beispiel: die Funktion f(x) = 0,5·x hat im Intervall[2|4] als höchsten Punkt den Punkt (4|2). Zwar gibt es außerhalb des Intervalls höhere Punkte, dass spielt aber keine Rolle. Im Intervall ist (4|2) der Hochpunkt. Siehe auch Intervall ↗
f'(x) ist zweitrangig
Die Vorstellung, dass ein Extrempunkt immer der Gipfel eines rundlichen Hügels oder die Sohle eines gerundeten Tales sein muss, ist falsch. Zwar sind solche Punkte immer auch (lokake) Extrempunkte und haben als Wert der ersten Ableitung f'(x) die 0. Aber keine der recherchierten Definitionen forderte dies als notwendige Bedingung für einen Extrempunkt. Beispiel: die sogenannte Betragsfunktion f(x)=|x| hat bei x=0 einen Tiefpunkt: der Graph sieht aus wie ein spitzes V mit dem tiefsten Punkt bei x=0. Dort ist der Graph nicht differenzierbar, es gibt keinen Wert für f'(x). Dennoch ist der Punkt nach allen Definitionen ein gültiger Tiefpunkt. Siehe auch hinreichende Bedingung ↗
Zwei Definitionen: sarke und schwache Extrempunkte
Manche Autoren[4] fordern, dass es zu einem Hochpunkt keinen gleich hohen und zu einem Tiefpunkt keinen gleich tiefen Punkt im betrachteten Intervall geben darf. Diese Definition ist die für die Schulmathematik meist übliche. Man könne von einem starken Extrempunkt sprechen. Andere Autoren[1][2][3] erlauben, dass ein Extrempunkt mehrere gleich hohe oder gleich tiefe Punkt im betrachteten Intervall (kollektiv) haben darf. Man könnte hier von einem schwachen Extrempunkt sprechen. Das führt jedoch zu der schwer akzeptierbaren Folge, dass alle Punkte einer konstanten Funktion, wie etwa f(x)=4 gleichzeitig Hoch- und auch Tiefpunkte sind. Die erste Definition, die hier auch vewendet wird, vermeidet diese kontraintuitive Folge.
- f(a) größer/kleiner als andere f(x) starker Extrempunkt [schulüblich] ↗
- f(a) größer/kleiner oder gleich anderer f(x) schwacher Extrempunkt ↗
Lokal und global
Unabhängig davon, ob man die schwache oder starke Form der Extrempunkte betrachtet, werden weiter globale (absolute) sowie lokale (relative) Extrempunkte unterschieden. Ein globaler Extrempunkt ist ein Extrempunkt in einem unendlich großen (z. B. Definitionsbereich) oder einem endlichen Intervall mit festen Rändern. Ein lokaler Extrempunkt ist ein Extrempunkt in einem beliebig kleinen Internvall ohne feste Rändern, einer sogenannten Epsilon-Umgebung.
- Absoluter Extrempunkt, heißt auch globaler Extrempunkt ↗
- Relativer Extrempunkt, heißt auch lokaler Extrempunkt ↗
Tipps
- Wende- und Sattelpunkte sind keine Extrempunkte.
- Ein Extrempunkt kann ein absolutes Maximum ...
- oder Minimum sein, muss es aber nicht.
- Scheitelpunkte von Parabeln sind immer Extrempunkte.
- Der x-Wert eines Extrempunkts heißt Extremstelle ↗
- Der y-Wert eines Extrempunkts heißt Extremwert ↗
Fußnoten
- [1] Der Extrempunkt ist gleich hoch/tief wie andere Punkte: Guido Walz: Spektrum Lexikon der Mathematik. Band 2: Eig bis Inn; 2001; ISBN: 3-8274-0437-7
- [2] Der Extrempunkt ist gleich hoch/tief wie andere Punkte: Wolfram MathWorld: https://mathworld.wolfram.com/Extremum.html (Dez 2020).
- [3] Der Extrempunkt ist gleich hoch/tief wie andere Punkte: Bronstein, Semendjawew, Musiol, Mühlig: Taschenbuch der Mathematik. 10. Auflage, 2016. ISBN: 978-3-8085-5789-1. Verlag Harri Deutsch.
- [4] Der Extrempunkt ist immer tiefer oder höher als andere Punkte: Lothar Papula: Mathematik für Ingenieure und Naturwissenschaftler. Ein Lehr- und Arbeitsbuch für das Grundstudium. 14. Auflage, 2019. ISBN: 978-3-658-0561-3. Verlag Springer Vieweg.