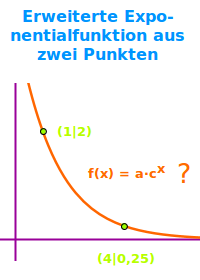
Erweiterte Exponentialfunktion aus zwei Punkten
f(x)=a·bˣ
Basiswissen
Man hat zwei oder mehr Punkte eines Graphen von einer Exponentialfunktion. Mit diesen Angaben kann man eine Funktionsgleichung erstellen. Gesucht sind die Koeffizienten a und b. Für sie sollen am Ende konkrete Zahlenwerte eingesetzt werden. Das Verfahren verläuft analog zum aufstellen einer Geradengleichung oder einer Parabelgleichung aus zwei Punkten: man setzt beide Punkte in die Grundform (Bauplan) der Funktionsgleichung ein. Dadurch ensteht ein lineares Gleichungssystem (LGS), das man dann löst. Die Ergebnisse des LGS sind die gesuchten Koeffizienten des Funktionstermes. Das Dach ^ steht für hoch. b^x meint dasselbe wie b-hoch-x.
Gesucht
- f(x) = a·b^x
- f(x) = a·bˣ
Tipps
- Im Ergebnis stehen für a und b dann konkrete Zahlen.
- Wenn mehr als zwei Punkte gegeben oder bekannt sind:
- Wähle am besten Punkte, die auf der x-Achse weit voneinander entfernt sind.
- Das gibt oft eine bessere Lösung für die restlichen Punkte.
Gegeben
- Gegeben:
- Punkt P(1|2)
- Punkt Q(4|0,25)
- 1 und 4 sind die x-Werte.
- 2 und 0,25 sind die f(x)-Werte.
Punkte einsetzen
- Punkt P einsetzen in f(x): I: 2 = a·b^1
- Punkt Q einsetzen in f(x): II: 0,25 = a·b^4
LGS lösen
- Das ist ein Gleichungssystem.
- I und II sind die beiden Gleichungen.
- Zum Lösen gibt es verschiedene Verfahren:
- Gleichsetzen, Einsetzen oder Additionsverfahren.
- Hier benutzt wird das Gleichsetzungsverfahren ↗
- Gleichsetzen über a[1] gibt:
- 2:(b^1) = 0,25:(b^4)
- Nach b auflösen gibt:
- b = 0,5
- b=0,5 einsetzen in I oder II gibt:
- a = 4
Antwort
- Fertige Funktionsgleichung hinschreiben:
- f(x) = 4·0,5^x ✔
Beispiele
- (0|0) und (1|2) ⭢ f(x) = 1·2^x
- (1|2) und (4|0,25) ⭢ f(x) = 4·0,5^x
- (1|50) und (3|12,5) ⭢ f(x) = 100·½^x
Fußnoten
- [1] Gleichsetzen über a heißt, dass man zuerste beide Gleichungen für sich alleine so umstellt, dass das a alleine auf der linken Seite des Gleichheitszeichens steht. Dann setzt man die beiden Terme rechts vom Gleichheitszeichen gleich. Siehe auch gleichsetzen über ↗