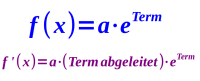e-Funktion ableiten
Anleitung
Basiswissen
f(x) = a·eᵀᵉʳᵐ ᵐⁱᵗ ˣ: wie man die erste Ableitung f'(x) bildet: Exponent von e ableiten multipliziert mit dem ursprünglichen Funktionsterm gibt die erste Ableitung f'(x).
Kurzbeispiele
- f(x) = e^(4x²-2x) ⭢ f'(x) = (8x-2)·e^(4x²-2x)
- f(x) = e^(4x) ⭢ f'(x) = 4·e^(4x)
- f(x) = e^x ⭢ f'(x) = e^x
- f(x) = 4e^x ⭢ f'(x) = 4e^x
Die gegebene Funktion f(x)
- f(x) = a·eᵀᵉʳᵐ ᵐⁱᵗ ˣ
- Man hat die Zahl e hoch irgendeinen Term mit x.
- Anders gesagt: das x taucht im Exponenten der Zahl e auch.
- Vor der Potenz eᵀᵉʳᵐ ᵐⁱᵗ ˣ darf ein konstanter Faktor (reiner Zahlenterm) stehen.
- Das e ist eine konstante Zahl (etwa 2,718) und heißt Eulersche Zahl ↗
- Siehe auch e-Funktion ↗
f(x) ableiten zu f'(x)
- Man hat ein e-Funktion: f(x) = a·eᵀᵉʳᵐ ᵐⁱᵗ ˣ
- Leite den Exponenten von e ab, und schreibe diese Ableitung auf.
- Setze eine runde Klammer um diesen abgeleiteten Exponenten.
- Schreibe dahinter einen Malpunkt
- Schreib dahinter den ursprünglichen Funktionsterm.
- Fertig ✔
Beispiele
- f(x) = ⅓·e⁹ˣ⁺⁵ ⭢ f'(x) = 9·⅓·e⁹ˣ⁺⁵
- f(x) = 2·e⁹ˣ ⭢ f'(x) = 18·e⁹ˣ
- f(x) = 5·eˣ ⭢ f'(x) = 5·eˣ
Tipp: es kommt kein x vor
- Es kommen manchmal auch Potenzterme ganz ohne x vor.
- Der Potenzterm besteht nur aus konstanten Zahlen.
- Zur Erinnerung: e selbst ist auch eine konstante Zahl.
- Konstante Zahlen abgeleitet ergeben immer 0.
- Beispiel: e⁹ gibt abgeleitet 0.
Kettenregel
- Die oben beschriebene Regel heißt auch Kettenregel.
- Man formuliert sie auch: f'(x) = innere Ableitung mal äußere Ableitung.
- Die innere Ableitung ist der Exponent, die äußere Ableitung der gesamte Funktionsterm.
- Siehe auch Ableiten über Kettenregel ↗
Produktregel
- Die Regel oben gilt nur, wenn das x nur auf einer Seite von einem Malzeichen steht.
- Steht das x aber auf zwei Seiten eines Malzeichens, gilt die Produktregel.
- Beispiel: f(x) = x·e⁹ˣ kann man nicht wie oben beschrieben ableiten.
- Man benötigt dazu die Produktregel ↗