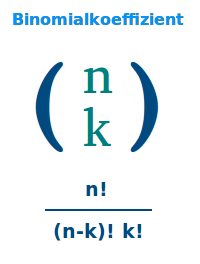Binomialkoeffizient
Formel
Definition
n über k = n! durch [k! mal (n-k)!]. Mit Zahlen: 5 über 3 gäbe 5! durch 3!·(5-3)!. Ausgerechnet gibt das genau 10. Die Berechnung wird hier ausführlich erklärt.
Sprechweise
- Die obere wird abgekürzt mit n.
- Die untere Zahl wird abgekürzt mit k.
- Man spricht: n über k, z. b. 6 über 4.
Formel
- n über k = n!/[k!·(n-k)!]
Legende
- Das n ist die Länger einer Bernoulli-Kette ↗
- Das k ist die Anzahl der Treffer in der Bernoulli-Kette.
- Das Ausrufezeichen ist eine Rechenart und heißt Fakultät ↗
Wie berechnet man das?
- Man setzt für n und k die Zahlenwerte ein in: n!/[k!·(n-k)!]
- Beispiel für n=5 und k=3: 5!/[(3!·(5-3)!]
- Dann rechnet man die Fakultäten aus:
- 120/[6·2] = 120/12 = 10 ✔
- Mehr unter n über k ↗
Wofür steht der Ausdruck anschaulich?
- Im Urnenmodell: Kombinationen ohne Zurücklegen
- Im Baumdiagramm: Anzahl Pfade mit gleichem Ausgang
- Im Binomischen Lehrsatz: Vorfaktor vor Gliedern
n über n
- Ein Zahl über sich selbst ist per Definition immer 1.
- 4 über 4 ist 1.
- 1 über 1 ist 1.
- 0 über 0 ist 1.
Über 0
- Irgendwas über 0 gibt per Definition immer 1.
- 5 über 0 ist 1.
- 0 über 0 ist 1.