Ableitung
f'(x)
Definition
Die Ableitung steht einmal für die Steigung (als Zahl) an einem bestimmten Punkt auf einem Funktionsgraphen. Präziser spricht man hier auch vom Ableitungswert. Als Ableitung bezeichnet man auch eine Funktion f'(x), die für jeden x-Wert die dort geltende Steigung am Graphen angibt.[1][2] Präziser wäre hier: Ableitungsfunktion
Ableitungswert
- Die Steigung eines Graphen an einer bestimmten x-Stelle nennt man den Ableitungswert.
- Der Graph von f(x)=x² hat an der Stelle x=2 die Steigung 4.
- Der Ableitungswert ist also die Zahl 4.
- Das ist die Steigung in einem Punkt ↗
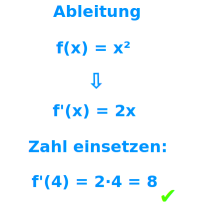
Ableitungsfunktion
- Eine Funktion f'(x) nennt man die Ableitungsfunktion.
- Setzt man einen x-Wert dort ein, dann ist der Funktionswert die Steigung von f(x) an der eingesetzen x-Stelle.
- Beispiel: die Ableitungsfunktion f'(x)=2x gehört zu Funktion f(x)=x².
- Setzt man die Zahl 2 in f'(x) ein, erhält man: f'(2)=6.
- Für jeden eingesetzten x-Wert erhält man die passende Steigung.
- Eine solche Funktion zu finden nennt man oft kurz ableiten ↗
Zahlenbeispiel für die erste Ableitung
- f(x) ist die eigentliche Funktion, z. B.: f(x) = x²
- Man kann von f(x) die sogenannte Ableitungsfunktion bilden:
- f(x) = x² gibt die Ableitungsfunktion: f'(x) = 2x
- Man kann nun irgendeinen x-Wert in f'(x) einsetzen.
- Beispiel f'(3) = 2·3 = 6.
- Die Zahl 6 ist der y-Wert von f'(x) bei x = 3.
- Der y-Wert von f'(x) ist gleichzeitig die Ableitung von f(x).
- Bei x=3 hat die ursprüngliche Funktion f(x) = x² also die Steigung 6.
- Mehr unter Steigung in einem Punkt ↗
Anschauliche Deutung der ersten Ableitung
Der y-Wert der Ableitung f'(x) an der Stelle xo ist die Steigung von f(x). Die Stelle xo meint hier den x-Wert eines Punktes auf dem Funktionsgraphen. Siehe auch erste Ableitung ↗
Bestimmung
- Zur Bestimmung der Ableitung gibt es mehrere Verfahren:
- Am gebräuchlichsten ist die Benutzung der Ableitungsfunktion ↗
- Sehr elementar ist die h-Methode bzw. das Sekantenverfahren ↗
Fußnoten
- [1] Das Spektrum Lexikon der Mathematik definiert die Ableitung als "lokale Annäherung einer Funktion durch eine lineare Abbildung". Für eine reelle Funktion gibt das Lexikon dann den Formalismus für das Ableiten über den Differentialquotienten (h-Methode) an. In: Das Spektrum Lexikon der Mathematik, online, Stand 13. September 2021: https://www.spektrum.de/lexikon/mathematik/ableitung-einer-funktion/499 Spektrum Lexikon der Mathematik ↗
- [2] Ableitung als Synonym für Ableitungsfunktion: Bronstein, Semendjajew, Musiol, Mühlig: Taschenbuch der Mathematik. 10. Auflage, 2016. ISBN: 978-3-8085-5789-1. Verlag Harri Deutsch. Seite 446. Siehe auch Der Bronstein ↗