Wendepunkte
Arten und Beispiele
Basiswissen
Es gibt LR- und RL-Wendepunkte sowie alle Sattelpunkte sind immer auch allgemeine Wendepunkte. Diese Arten und auch einige allgemeine Beispiele sind hier kurz vorgestellt.
Kurzinfo
Wendepunkte sind Punkte auf Funktionsgraphen. An diesen Punkten ändert sich die Richtung der Kurvenkrümmung. Die Krümmung kann von links auf rechts oder von rechts auf links wechseln. Wendepunkte gehören nicht zu den Extrempunkten. Ein Wendepunkt mit der Steigung Null heißt auch Sattelpunkt. Weiter unten folgen Arten und Beispiele. Eine Definition und Übersicht steht auf Wendepunkt ↗
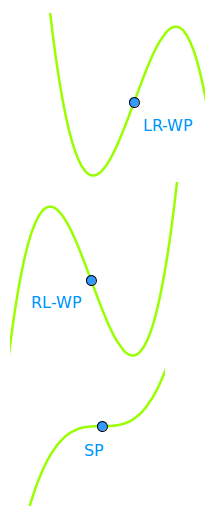
LR-Wendepunkt
Die Krümmung wechelt von links auf rechts: Linkskrümmung ist im Graphen wie eine nach oben offene Schüssel. Rechtskrümmung ist wie eine nach unten offene Schüssel. Der Wert der ersten Ableitung ist uwichtig. Die zweite Ableitung muss immer 0 sein. Lies mehr unter LR-Wendepunkt ↗
RL-Wendepunkt
Die Krümmung wechelt von rechts auf links: Linkskrümmung ist im Graphen wie eine nach oben offene Schüssel. Rechtskrümmung ist wie eine nach unten offene Schüssel. Der Wert der ersten Ableitung ist unwichtig. Die zweite Ableitung muss immer 0 sein. Lies mehr unter LR-Wendepunkt ↗
Sattellpunkt
Ein Sattelpunkt ist ein Wendepunkt mit der Steigung Null: für den entsprechenden x-Wert müssen die erste und die zweite Ableitung beide Null ergeben. Ein Sattelpunkt kann ein LR- oder auch ein RL-Wendepunkt sein. Lies mehr unter Sattelpunkt ↗
Kubische Funktionen
- f(x) = x³ | WP (0|0)
- f(x) = x³ + 1 | WP (0|1)
- f(x) = x³ - 3x² - 24x + 26 WP (1|0)
- f(x) = 2x³ + 9x² + 12x | WP (-1,5|-4,5)
- Siehe auch kubische Funktionen ↗
Quartische Funktionen
- f(x) = x⁴ - 2x³ | WP1 (1|-1) | WP2 (0|0)
- f(x) = x⁴ - 18x² - 12 | WP1 (-Wurzel 3|-57) | WP2 (Wurzel 3|-57)
- Siehe auch quartische Funktionen ↗