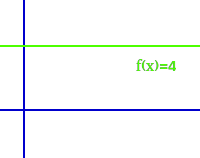
Waagrechte Gerade
Funktionsgraph
Basiswissen
Waagrecht heißt hier: von links nach rechts in einem xy-Koordinatensystem. Damit verläuft die Gerade parallel zur x-Achse. Ein typisches Beispiel ist: f(x)=4
Definition
- Gerade meint hier: Gerade in einem 2D-Koordinatensystem ↗
- Waagrecht meint: läuft parallel zur x-Achse.
- Die Gerade hat also überall dieselbe Höhe.
- Die Gleichung hat die Form: f(x)=Zahl
- Sie gehört zu einer konstanten Funktion.
Warum ist die Funktion nicht linear?
- Eine konstante Funktion gilt nicht als lineare Funktion.
- Eine lineare Funktion hat als Graph auch ein Gerade, aber:
- Linear sind nur Funktionen, deren Funktionsgleichung ...
- man in die Form f(x)=mx+b bringen kann.
- Dabei darf das b irgendeine Zahl sein, auch Null.
- Die Steigung m aber darf nicht 0 sein.
- Es muss also einen Term mit x geben.
- Bei einer waagrechten Geraden wäre die Funktionsgleichung ...
- immer f(x) = b, zum Beispiel: f(x)=4.
- Es gibt keinen Term mit x.
- Also ist f(x)=4 nicht linear.
Welcher Funktionstyp ist es dann?
- Funktionen mit der Gleichung f(x)=b heißen konstant.
- Konstante Funktionen haben als Graph immer eine waagrechte Gerade.
- Konstante Funktionen haben immer überall die Steigung 0.
- Mehr unter Konstante Funktion ↗
Was ist eine Ortslinie?
- Waagrechte Geraden kann man auch als Ortslinien betrachten.
- Ortslinien sind die Veranschaulichungen von Lösungen von Gleichungen.
- Eine solche Ortslinie hat eine Geradengleichung mit zwei Unbekannten ↗