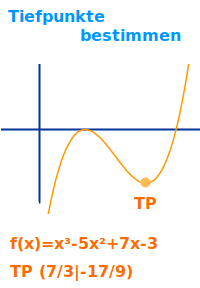
Tiefpunkte bestimmen
Lokale Tiefpunkte über Ableiten berechnen | Definition unter => Tiefpunkt
Basiswissen
Es werden verschiedene Methoden vorgestellt: graphisch, über f'(x) und als Scheitelpunkt einer Parabel.
Was sind Tiefpunkte
◦ Tiefpunkte sind Punkte auf einem Funktionsgraphen.
◦ Der x-Wert alleine heißt auch => Tiefstelle
◦ Der y-Wert alleine heißt auch => Tiefwert
◦ Beides zusammen gibt den => Tiefpunkt
◦ Definition unter => Tiefpunkt
Was meint "bestimmen"?
◦ Bestimmen meint: irgendwie herausfinden.
◦ Das kann rechnerisch, graphisch, über Raten oder sonstwie sein.
◦ Bestimmt werden der x- und der y-Wert.
Graphisch
◦ Erzeuge irgendwie einen Graphen.
◦ Finde Punkte die wie tiefste Stellen von einem Tal aussehen ...
◦ Bestimme den x- und y-Wert durch ablesen. Das gibt den Tiefpunkt.
◦ Siehe auch => 2D-Punkt aus Koordinatensystem
Über Ableiten
◦ Man bildet f'(x) und setzt es gleich 0.
◦ Nach x auflösen liefert mögliche Tiefstellen.
◦ x-Werte in f''(x) einsetzen. Falls das eine Zahl ...
◦ größer als 0 gibt, hat man eine Tiefstelle.
◦ x-Stelle in f(x) einsetzen gibt den => Tiefwert.
◦ x-Stelle und Tiefwert zusammen sind der Hochpunkt.
◦ Ausführlich unter => Tiefpunkte über Analysis
Legende
◦ f => eigentliche Funktion
◦ f' => erste Ableitung
◦ f'' => zweite Ableitung
Parabeln
◦ Parabeln sind die Graphen einer quadratischen Funktion.
◦ Ist die Parabel nach oben geöffnet, hat sie immer einen Tiefpunkt.
◦ Der Tiefpunkt einer Parabel heißt auch Scheitelpunkt.
◦ Mehr unter => Scheitelpunkt einer Parabel bestimmen
