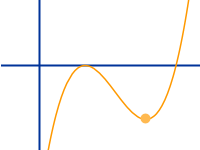
Tiefpunkte
… Arten und Anzahlen | siehe auch Tiefpunkte bestimmen ↗
Kurzinfo
Innerhalb der Analysis sind Tiefpunkte die in ihrer Umgebung tiefsten Punkte eines Graphen. In ihrer Umgebung heißt, dass man einen beliebig kleinen Bereich links und rechts des Punkte angeben kann, in dem es keine gleich tiefen oder tieferen Punkte gibt. Das Fremdwort für „in der näheren Umgebung“ ist lokal. Jeder Tiefpunkt ist damit per Definition ein lokaler Tiefpunkt. Ist er darüberhinaus der überhaupt tiefste Punkt des Graphen im Definitionsbereich oder einem ausgewählten Intervall, so nennt man ihn den globalen Tiefpunkt in diesem Bereich. Verschiedene Funktionsarten können unterschiedlich viele Tiefpunkte haben. Zur weiteren Definition siehe auch unter Tiefpunkt ↗
Global
- Globale Tiefpunkt sind die tiefsten Punkte im Definitionsbereich.
- Sie heißen auch absolute Tiefpunkte.
- Siehe auch globaler Tiefpunkt ↗
Lokal
- Alle direkten Nachbarn habe höhere y-Werte.
- Heißen auch relative Tiefpunkte.
- Mehr unter lokaler Tiefpunkt ↗
Funktionsarten
- Konstante Funktionen: 0
- Lineare Funktionen: 0
- Quadratische Funktion: 1
- Kubische Funktion: höchstens 2
- Quartische Funktion: höchstens 3
- Ganzrationale Funktion: höchstens so viele wie der höchste Exponent (von x) minus eins
Beispiele
- f(x) = x² hat lokalen TP bei (0|0)
- f(x) = x²-4 hat lokalen TP bei (0|-4)
- f(x) = x³-3x hat lokalen TP bei (1|2)
- f(x) = x^4-8x^2 hat lokalen TP bei (-2|-16) und (2|16)