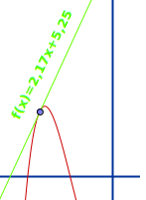
Tangentengleichung
Geradengleichung mit gleicher Steigung wie f(x)
Basiswissen
Definition: Eine Tangente t(x) ist immer eine Gerade, die einen Punkt mit einem anderen Graphen f(x) gemeinsam hat. Die Tangente und der Graph haben an diesem Punkt dieselbe Steigung. Es wird erklärt, was genau eine Tangente im Zusammenhang mit Graphen ist und wie man ihre Gleichung aufstellt.
Gegeben
- Man hat eine Funktionsgleichung f(x) gegeben.
- Oder man hat nur den Graphen einer Funktion gegeben.
- Zusätzlich ist noch ein Punkt auf dem Graphen gegeben.
- Beispiel: auf dem Graphen f(x)=x² liegt P(3|9).
Tangente
- Man stellt sich irgendeine Gerade durch den Punkt P vor.
- Dann dreht man die Gerade so lange, bis sie dieselbe Steigung hat wie f(x).
- Diese Steigung meint hier: dieselbe Steigung genau an dem Punkt P.
Tangentengleichung
- Die Tangentengleichung ist die Gleichung der Geraden, also der Tangente.
- Man nennt sie oft t(x) und schreibt sie als t(x)=mx+b
- Für den Punkt P(3|9) von f(x)=x² wäre das:
- t(x)=6x-9 ✔
Aufstellen
- Aufstellen meint hier so viel wie bestimmen oder berechnen.
- Das wird meistens über die erst Ableitung von f(x) gemacht.
- Mehr dazu unter Tangentengleichung aufstellen ↗