Statistische Abhängigkeit über Vierfeldertafel
Bestimmung
Basiswissen
Man hat eine Vierfeldertafel mit den relativen Häufigkeiten zu zwei Merkmalen. Man kann dann recht einfach überprüfen, ob die zwei Merkmale zueinander perfekt statistisch unabhängig sind oder nicht. Das ist hier ausfühlich erklärt.
Grundidee
- Hat man eine Vierfeldtafel mit relativen Häufigkeiten, ...
- dann kann man leicht die statistische Abhängigkeit überprüfen.
- Das wird hier an einem Beispiel erklärt.
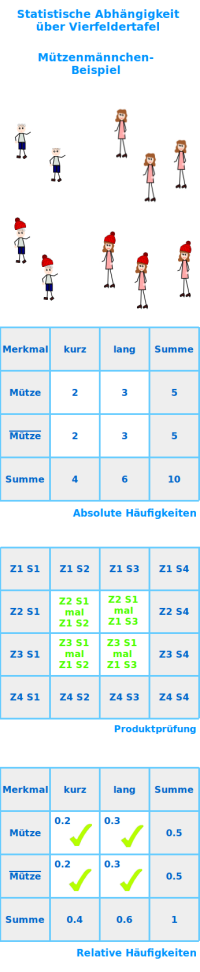
Mützenmännchen
- Zeichne 4 kurze Strichmännchen.
- Zeichne 6 lange Strichmännchen.
- Setze 2 der kurzen Strichmännchen eine Mütze auf.
- Setze 3 der langen Strichmännchen eine Mütze auf.
Vierfeldertafel
- Zeichne eine Tabelle mit 4 Zeilen und 4 Spalten.
- Zeilen gehen von links nach rechts.
- Spalten gehen von oben nach unten.
- Die Tabelle hat 16 Felder.
- Trage in die Felder ein:
- 1. Zeile, 1. Spalte: nichts eintragen.
- 1. Zeile, 2. Spalte: k (für "kurz").
- 1. Zeile, 3. Spalte: l (für "lang").
- 1. Zeile, 4. Spalte: Summe
- 2. Zeile, 1. Spalte: M (für "Mütze")
- 2. Zeile, 2. Spalte: 0,2
- 2. Zeile, 3. Spalte: 0,3
- 2. Zeile, 4. Spalte: 0,5
- 3. Zeile, 1. Spalte: M durchgestrichen ("Keine Mütze")
- 3. Zeile, 2. Spalte: 0,2
- 3. Zeile, 3. Spalte: 0,3
- 3. Zeile, 4. Spalte: 0,5
- 4. Zeile, 1. Spalte: Summe
- 4. Zeile, 2. Spalte: 0,4
- 4. Zeile, 3. Spalte: 0,6
- 4. Zeile, 4. Spalte: 1,0
Überprüfung allgemein
- Du musst vier Bedingungen überprüfen.
- Treffen alle zu, sind die zwei Merkmale statistisch unabhängig.
- Treffen nicht alle zu, sind die Merkmale statistisch abhängig.
- (Die Kürzel Z2 oder S4 meinen "Zeile 2" oder "Spalte 4".)
- 1. Bedingung: Z2S4 mal Z4S2 = Z2S2
- 2. Bedingung: Z2S4 mal Z4S3 = Z2S3
- 3. Bedingung: Z3S4 mal Z4S2 = Z3S2
- 4. Bedingung: Z3S4 mal Z4S3 = Z3S3
Überprüfung Mützenmännchen
- 1. Bedingung: 0,5 mal 0,4 = 0,2 ⭢ passt
- 2. Bedingung: 0,5 mal 0,6 = 0,3 ⭢ passt
- 3. Bedingung: 0,5 mal 0,4 = 0,2 ⭢ passt
- 4. Bedingung: 0,5 mal 0,6 = 0,3 ⭢ passt
Folgerung
Es gehen alle vier Bedingungen auf. Also sind Körperlänge und Mützentragen statistisch unabängig (externer Link)
Tipp
- Diese Methode funktioniert nicht mit den absoluten Häufigkeiten.
- Sie geht nur mit Prozenten, Anteilen oder Bruchteilen ...
- (also nur mit relativen Häufigkeiten).
- Siehe auch relative Häufigkeit ↗