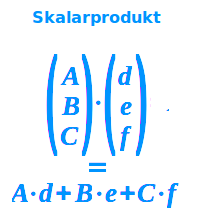Skalarprodukt
Übersicht
Definition
(1|2|3) skalar multipliziert mit (2|2|2) gibt 1·2+2·2+3·2 und als Zahl die 12: das Skalarprodukt, auch inneres Produkt genannt, für zwei Vektoren ist hat als Ergebnis immer nur eine reine Zahl. Das ist hier ausführlich erklärt.
Was ist ein Skalar?
- In der Mathematik meint Skalar eine reine Zahl.
- Ein Vektor oder eine Matrix sind kein Skalar.
- Skalare sind Zahlen wie: 3; -0,5 oder ½
- Siehe auch Skalar ↗
Schreibweisen
Als Platzhalter für Vektoren werden normalerweise lateinische Kleinbuchstaben verwendet. Dass sie für Vektoren stehen sollen, kann man auf zwei Arten deutlich machen: man setzt einen kleinen Rechtspfeil über den Buchstaben. Oder aber man schreibt den Buchstaben kursiv (englisch: italic). Für das Skalarprodukt gibt es verschiedene Schreibweisen. Wichtig ist, eine Verwechslung mit dem Vektor- oder Kreuzprodukt zu vermeiden. Für das Skalarprodukt sind die folgenden Schreibweisen typisch.
- 𝑣⋅𝑤
- 𝑣∘𝑤
- 𝑣∙𝑤
- (𝑣,𝑤)
- ⟨𝑣|𝑤⟩
Skalarprodukt
- Man kann Vektoren auf verschiedene Weisen miteinander multiplizieren.
- Dabei kann das Ergebnis ein Vektor oder auch nur eine Zahl sein.
- Ist das Ergenbnis nur eine Zahl, spricht man vom Skalarprodukt.
Skalarprodukt berechnen
- Man schreibt die zwei Vektoren senkrecht nebeneinander.
- Dann multipliziert man alle Zahlen, die auf derselben Höhe stehen, also nebeinander.
- Diese Zwischenergebnisse addiert man dann als Plusrechnung alle auf.
- Das Ergebnis ist dann das Skalarprodukt.
- Mehr unter Skalarprodukt berechnen ↗
Skalarprodukt und Winkel
- Das Skalarprodukt hängt eng mit dem Winkel zwischen Vektoren zusammen.
- Stehen zwei Vektoren senkrecht aufeinander, gibt ihr SP immer 0.
- Ist das SP zweier Vektoren Null, stehen die Vektoren senkrecht aufeinander.
- Einzige Ausnahme: wenn einer der Vektoren der Nullvektor ist.
- SP = Länge erster Vektor · Länge zweiter Vektor · cos von Alpha
- Alpha ist der (kleinste) Winkel zwischen den beiden Vektoren
- Siehe auch Winkel über Skalarprodukt ↗
Skalarprodukt anschaulich
- Man bildet das Skalarprodukt zweier Vektoren a und b.
- Das Skalarprodukt ist als Zahlenwert dann immer gleich ...
- dem Produkt der Länge von a und der Länge der Projektion von b auf a.
- Mehr dazu unter Skalarprodukt anschaulich ↗
Orthogonalität von Vektoren
- Orthogonal heißt: mit 90-Grad-Winkel ↗
- Man soll überprüfen, ob zwei Vektoren senkrecht aufeinander stehen.
- Gibt ihr Skalaprodukt 0, sind die Vektoren senkrecht zueinander.
- Beispiel: Man hat die Vektoren (2|6|-5) und (9|2|6).
- Das Skalarprodukt ist 2·9 + 6·2 + (-5)·6 = 0
- Die Vektoren sind senkrecht zueinander.
- Siehe auch orthogonal ↗
Gilt das Kommutativgesetz?
- Ja, Vektor a mal Vektor b ist dasselbe wie Vektor b mal Vektor a skalar multiplziert.
- Siehe auch Skalarprodukt aus drei Vektoren ↗
Gilt das Assoziativgesetz?
- Nein, und zwar weil Klammern mindestens drei Vektoren benötigen, das Skalarprodukt dafür aber nicht definiert ist.
- Man betrachte als Beispiel die drei identischen Vektor a, b und c mit den Komponenten (1 2 3).
- a·b gäbe eine Zahl. Diese Zahl würde dann mit c multipliziert.
- Damit wäre der zweite Malpunkt aber keine skalare Multiplikation mehr.
- Denn: Zahl mal Vektor gibt wieder einen Vektor.
- Das Skalarprodukt von drei Vektoren ist nicht definiert ↗
Gilt das Distributivgesetz?
- Ja:
- Die drei identischen Vektoren a, b hätten beispielhaft die Komponenten: (1 2 3)
- Dann müsste gelten: a·(b+c) = a·b + a·c
- a·(b+c) gibt ausgerechnet genau: 28
- Auch a·b+a·c gibt genau 28.
- Siehe auch Distributivgesetz ↗