Scheitelpunktform aus zwei Punkten
Anleitung
Basiswissen
Der Scheitelpunkt SP und anderer Punkt einer Parabelgleichung (quadratische Funktion) sind gegeben. Gesucht ist die Funktionsgleichung in Scheitelpunktform: f(x)=a(x-d)²+e
Was meint Scheitelpunktform?
- Das ist eine von mehreren Formen einer Parabelgleichung ↗
- Parabelgleichung meint hier dasselbe wie quadratische Funktion ↗
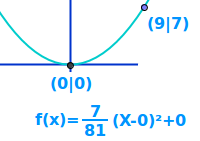
- Scheitelpunktform: f(x) = a(x-d)² + e
Legende
- f(x) = y-Wert eines Punktes auf der Parabel
- a = Streckungsfaktor der Parabel
- d = x-Wert des Scheitelpunktes
- e = y-Wert des Scheitelpunktes
Was muss gegeben sein?
- Es müssen mindestens zwei Punkte gegeben sein.
- Gegeben heißt: man kennt ihre x- und y-Werte.
- Einer der Punkte muss der Scheitelpunkt sein.
- Zum Beispiel: (1|2) als Scheitelpunkt und ...
- (3|10) als anderer Punkt.
1. Schritt
- Scheitelpunkt einsetzen:
- Man nimmt die Scheitelpunktform: f(x) = a(x-d)² + e
- Man nimmt den x-Wert des gegebenen Scheitelpunktes.
- Man setzt ihn für das d oben ein.
- Man nimmt den y-Wert des Scheitelpunktes.
- Man setzt ihn für e ein.
- Das gibt: f(x)=a(x-1)²+2
2. Schritt
- Anderen Punkt einsetzen:
- Man nimmt das Zwischenergebnis aus Schritt 1:
- Man hat also: f(x)=a(x-1)²+2
- Man nimmt den zweiten gegebenen Punkt.
- Das ist hier im Beispiel: (3|10)
- Man setzt seinen x-Wert für x,
- und seinen y-Wert für f(x) in
- das Zwischenergebnis ein:
- 10 = a(3-1)²+2
3. Schritt
- Nach a auflösen:
- Zuerst klammer ausrechnen: 3-1 gibt 2.
- Dann den Klammerwert (hier 2) quadrieren, gibt: 4
- Zwischenstand: 10 = a·4+2 | -2
- Gibt: 8 = 4a | :2
- Gibt: a=2
4. Schritt
- Ergebnis aufschreiben:
- Man hat jetzt die Werte für a, d und e bestimmt.
- a = 4
- d = 1
- e = 2
- Damit schreibt man die Scheitelpunktform auf:
- Im Beispiel wäre das:
- f(x) = 2(x-1)²+2
Trainingsaufgaben dazu
Einige Aufgaben mit Lösungen sind hier als Quickcheck zusammengestellt. Direkt zu den Aufgaben geht es über => qck
Gibt es noch andere Verfahren?
Ja, man kann die Scheitelpunktform auch aus drei Punkten oder aus gegebenen anderen Formen aufstellen. Eine Übersicht zu allen Verfahren steht im Artikel Scheitelpunktform aufstellen ↗