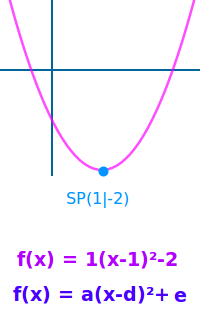
Scheitelpunktform
f(x) = a·(x-d)² + e
Basiswissen
Die Scheitelpunktform gehört zu den Themen quadratische Funktionen und Parabeln. Aus ihr kann man leicht den Scheitelpunkt, die Öffnung und den y-Achsenabschnitt ablesen. Umgekehrt kann man sie leicht aufstellen, wenn man von einer Parabel den Scheitelpunkt SP und irgendeinen weiteren Punkt kennt. Das ist im Folgenden beschrieben.
Definitionen
- Der Scheitelpunkt einer Parabel ist ihr höchster oder ihr tiefster Punkt.
- Die Scheitelpunktform gilt für quadratische Funktionen:
- Eine Zahl a mal einer Klammer zum Quadrat und am Schluss plus oder minus eine Zahl.
- In der Klammer steht x plus oder x minus eine Zahl.
Wie liest man den Scheitelpunkt ab?
- Hat man eine quadratische Funktion in die Scheitelpunktform gebracht, ...
- dann kann man den Scheitelpunkt direkt ablesen.
- So sieht die Form aus: f(x) = a(x-d)² + e
- Wichtig: in der Klammer muss ein "Minus" stehen.
- Der Scheitelpunkt S ist dann immer (d|e).
- Steht in der Klammer ein Minus, ist d eine Pluszahl.
- Steht in der Klammer ein Plus, ist d eine Minuszahl.
- Mehr unter Scheitelpunkt aus Scheitelpunktform ↗
Was bedeuten das a, d und e?
- Das a gibt die Stauchung/Streckung an.
- Positives a: nach oben geöffnet
- Negatives a: nach unten geöffnet
- Das d ist der x-Wert des Scheitelpunktes.
- Das e ist der y-Wert des Scheitelpunktes.
Beispiele
- f(x) = 4(x+3)²+14, der SP ist dann (-3|-14)
- f(x) = 0,5(x-5)²-3, der SP ist dann (5|-3)
Transformationen
- Transformation meint hier eine Veränderungen ...
- des Graphen im Vergleich zur Normalparabel:
- a kleiner als -1: gestreckt, nach unten geöffnet
- a zwischen -1 und 0: gestaucht, nach unten geöffnet
- a zwischen 0 und 1: gestaucht, nach oben geöffnet
- a größer als 1: gestreckt, nach oben geöffnet
- d positiv: nach links verschoben
- d negativ: nach rechts verschoben
- e positiv: nach oben verschoben
- e negativ: nach unten verschoben