Nullstellen von ganzrationalen Funktionen
Einführung zu dem Thema
Basiswissen
Lineare, quadratische, kubische Funktionen und so weiter nennt man ganzrational. Eine solche Funktion hat höchstens so viele Nullstellen, wie der höchste Exponent von x ist. Hier steht eine kurze Einführung ins das Thema. Zur Berechnung siehe unter Nullstellen von ganzrationalen Funktionen bestimmen ↗
Was sind ganzrationale Funktionen?
- Das sind Funktionen, bei denen das x nur natürlichzahlige Exponenten hat.
- Beispiele: f(x) = 4x³-5x³+17x-24 oder auch f(x) = 5 oder f(x) = 2x²
- Tipp: eine Zahl wie 24 wäre wie 24·x^0. Die 0 ist als Exponent auch erlaubt.
Wie sehen die Graphen dieser Funktionen aus?
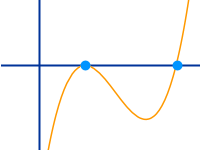
- Der Graph so einer Funktion ist entweder eine Gerade ...
- oder ein geschwungene Kurvenlinie.
- Es gibt nie Lücken oder Knicke.
Was sind Nullstellen?
- Das sind die x-Werte bei denen f(x) zu 0 wird.
- Im Graph sind das die x-Achsenabschnitte.
- Also wo der Graph die x-Achse schneidet.
Wie viele NS haben diese Funktionen?
- Das hängt vom höchsten Exponenten (Hochzahl) von x ab.
- Es gibt höchstens so viele NS wie der höchste Exponent von x groß ist.
- Gibt es nur geradzahlige Exponenten von x kann es auch gar keine NS geben.
- Ausnahme: Die Nullfunktion f(x) hat den Exponenten 0 und...
- trotzdem unendlich viele Nullstellen.
Wie gibt man Nullstellen an?
- Es gibt verschiedene Arten.
- Nehmen wir f(x) = x³-x² als Beispiel.
- Auf Deutsch: Es gibt NS bei x=0 und bei x=1.
- Man kann auch die Punktschreibweise angegeben.
- Punktschreibweise: N1(1|0) und N2(0|1).
Welche Beispiele gibt es?
- f(x) = 4 hat gar keine NS.
- f(x) = x hat bei x=0 eine NS.
- f(x) = x²+17 hat gar keine NS.
- f(x) = x³-27 hat bei x=3 eine NS.
Wozu braucht man das?
- In der höheren Mathematik braucht man die NS fast überall.
- Ein praktisches Beispiel: Wie hoch und breit muss eine Ravioli-Dose sein, ...
- sodass sie für 800 ml Inhalt möglichst wenig Blech braucht? Das zu lösen geht über NS.
Wie findet man die Nullstellen?
- Das ist ein großes Thema mit einer eigenen Seite.