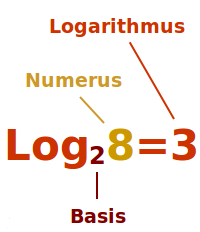
Logarithmusgleichungen lösen
Verfahren
Basiswissen
Es gibt drei Grundfälle, unterschieden danach, wo die Unbekannte steht. Alle drei Fälle werden hier besprochen.
Logarithmus ist unbekannt
- Der Logarithmus ist die Zahl rechts vom Gleichzeichen.
- In der Potenzdenkweise ist der Logarithmus der Exponent.
- Beispiele: lg 1000 = x oder lb 8 = x oder ln e = x
- Zum Lösen: linke Seite in Taschenrechner eintippen.
Numerus ist unbekannt
- Der Numerus ist die Zahl direkt hinter log, lg, lb oder ln:
- In der Potenzdenkweise ist der Numerus der Potenzwert.
- Beispiele: lg x = 3 oder lb x = 8 oder ln x = 2
- Lösungstipp: in Potenzschreibeweise umformen:
- lg x = 3 wäre in Potenzschreibweise 10³=x, das einfach ausrechnen
Basis ist unbekannt
- Die Basis steht oft klein unten rechts vom log.
- In der Potenzdenkweise heißt sie auch Basis.
- Beispiel: log von 64 zu welcher Basis ist 3?
- Lösungstipp: in Potenzschreibweise umformen: x³=64
- Auf beiden Seiten die 3 Wurzel ziehen gibt: x=4.
- Mehr unter Logarithmusgleichung mit x in Basis lösen ↗
Tipps
- lg meint Logarithmus zur Basis 10
- lb meint Logarithmus zur Basis 2
- ln meint Logarithmus zur Basis e
- Numerus ist die Zahl direkt hinter lg, lb, ln oder log.
- Die Basis wird meistens nicht geschrieben. Sie ist implizit.
- Bei lg ist die Basis 10, bei lb die 2 und bei ln die Zahl e.
- Bei log wird die Basis klein rechts unterhalb von log geschrieben.
Ist die Einteilung oben allgemeingültig?
- Nein, das Wort Logarithmusgleichung wird uneinheitlich verwendet.
- Im engeren Sinn meint es nur Gleichungen mit unbekannten Numerus.
- Im schulmathematischen Sinn ist damit jede Gleichung mit log gemeint.
Beispiellösungen
- lb(x)=10, Lösung: x=1024
- lb(x)=-1, Lösung: x=0,5
- lg(x)=3, Lösung: x=1000
- lg(x+1)=3, Lösung: x=1001
- ln(x)=2, Lösung: x=e²
- ln(x-5)=2; Lösung: x=e²+5