Heron-Verfahren
Wurzelziehen
Basiswissen
Die Wurzel von 16 ist 4, denn 4·4 gibt 16. Aber was ist die Wurzel von der Zahl 6? Das Ergebnis ist eine sogenannte irrationale Zahl. Man kann sie also niemals exakt als Dezimalzahl angeben. Man kann sie aber mit beliebig vielen Nachkommastellen berechnen. Dazu dient das Heron-Verfahren.
Grundidee
Angenommen, aus der Zahl 16 soll die Quadratwurzel gezogen werden. Das Ergebnis muss die Zahl 4 sein. Angenommen, dieses Ergebnis ist einem noch nicht bekannt. Man wählt dann irgendeine beliebige positive Zahl, zum Beispiel die Zahl 2. Das ist dann der Wert xn. Man setzt diese Startzahl dann in den folgenden Term T ein:
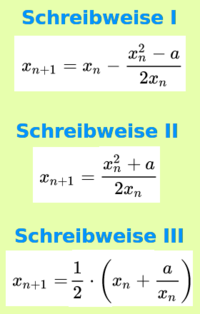
- T(xn) = xn - [(xn)²-a]/(2xn)
Das Ergebnis dieser Rechnung ist dann der neue Wert für xn, man nennt es auch xn+1. Man setzt diesen neuen Wert dann auch erneut in den Berechnungsterm T(xn) ein. Mit jeder neuen solchen Berechnung kommt man näher an die gesuchte Wurzel heran. Man bricht das Verfahren ab, wenn man die gesuchte Wurzel auf ausreichend viele Nachkommastellen berechnet hat.
Ein Zahlenbeispiel
- a = 16 ist die gesuchte Zahl, gesucht ist ihre Quadratwurzel ↗
- xn = 2 ist ein zufällig gewählter Wert für xn, also der Startwert ↗
- a=16 und xn=2 einsetzen in T(xn) = xn - [(xn)²-a]/(2xn)
- T(2) = 2-[2²-16]/(2·2) = 2-(-3) = 5
- Die 5 ist dann das neue xn und man rechnet neu:
- T(5) = 5-[5²-16]/(2·5) = 5-(0,9) = 4,1
- Die 4,1 ist dann das neue xn und man rechnet neu:
- T(4,1) = 4.0012195121951 ✔
Man sieht an diesem Zahlenbeispiel, wie schnell sich die Näherungslösung der exakten Lösung 4 annähert. Nach nur wenigen sogenannten Iterationsschritten hat man meist eine Lösung, die ausreichend genau ist. Verblüffend ist dabei, dass man als Startzahl jede beliebige positive Zahl nehmen kann. Trotzdem wird das Verfahren nach einigen Schritten sehr genau die Wurzel angeben. In der Mathematik bezeichnet man ein solcher Verhalten von Näherungsformeln als Konvergenz ↗
Was ist ein Algorithmus?
Als Algorithmus bezeichnet man ein starres Rechenverfahren, dass mit denselben Schritten immer auch zu demselben Ergebnis kommt. Man erkennt Algorithmen daran, dass man sie als starre Computerprogramme umsetzen kann. Das Heron-Verfahren ist ein solcher Algorithmus ↗