Geradengleichung aus Graph über Steigung und Punkt
Anleitung
Basiswissen
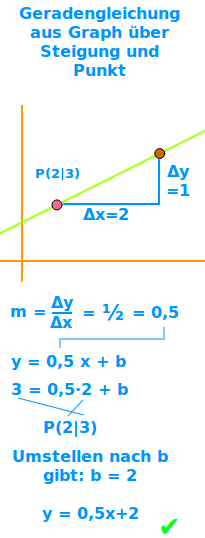
Wie man zum Beispiel y = 0,5x + 2 aus einem Graphen erstellt: es gibt die Methode über zwei Punkte oder über den y-Achsenabschnitt und das Steigungsdreieck. Beides ist hier kurz vorgestellt.
Ziel
- Man hat einen Graphen.
- Man hat dazu noch keine Gleichung.
- Die Gleichung y=mx+b ist gesucht.
- Man sucht die Zahlen für m und b.
- m ist die Steigung.
- b ist der y-Achsenabschnitt.
Steigungsdreieck
- Zeichne irgendwo auf der Geraden zwei Punkte.
- Ideal ist es, wenn sie auf "glatten" x- und y-Werten liegen.
- Zeichne quer durch den linken Punkt eine waagrechte Linie.
- Waagrecht meint: von links nach rechts.
- Zeichne durch den rechten Punkt eine senkrechte Linie.
- Senkrecht meint: von oben nach unten.
- Zeichne beide Linien so lange, dass sie sich treffen.
- Die Strecke vom linken Punkt bis zum Schnittpunkt heißt: Δx
- Die Strecke vom rechten Punkt bis zum Schnittpunkt heißt: Δy
- Schreibe die Länge von Δy an die senkrechte Strecke.
- Schreibe die Länge von Δx an die waagrechte Strecke.
Steigung m
- Teile Δy durch Δx.
- Das Ergebnis ist die Steigung m.
- Setze diese Zahl ein für m in: y=mx+b
y-Achsenabschnitt b
- Nimm irgendeinen Punkt auf der Geraden.
- Gehe senkrecht von ihm auf die x-Achse.
- Die Zahl dort ist der x-Wert des Punktes.
- Gehe waagrecht vom Punkt zur y-Achse.
- Die Zahl dort ist der y-Wert.
- Setze die Werte in y=mx+b ein.
- Jetzt ist nur noch b unbekannt.
- Stelle die Gleichung um nach b.
- Damit ist die Zahl für b bestimmt.
Schluss
- Man kennt jetzt den Zahlenwert von m und b.
- Schreibe y=mx+b damit auf. x und y bleiben Buchstaben.
- Beispiel y=0,5x+2.