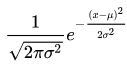Gauß-Funktion
Stochastik
Basiswissen
Eine Mathematische Funktion für normalverteilte Zufallsdaten: mit dieser Funktion kann man unter anderem Bernoulli-Ketten sehr großer Länge berechnen sowie - eng damit verwandt - Daten einer sogenannten Normalverteilung. Die Funktion ist hier mit ihrem eigentlich Zweck und Sinn kurz vorgestellt.
Gleichung
- φ(x) = 1/[√(2·π·σ²)] · e hoch [-0,5·(x-μ)²/σ²]
Legende
- φ = Name der Funktion kleines phi ↗
- √ = die Wurzel Wurzelzeichen ↗
- μ = kleines mü, der Erwartungswert ↗
- π = etwa 3,14, die Kreiszahl ↗
- σ = kleines sigma, die Standardabweichung ↗
- σ² = ist die Varianz ↗
Graph
- Der Graph heißt umgangssprachlich Glockenkurve ↗
- Fläche unter Kurve ist die Wahrscheinlichkeit für x-Werte im x-Intervall
Zweck
Die Gauß-Funktion kann benutzt werden, um binomialverteilte Zufallsgrößen (z. B. Anzahl Sechser bei n Würfel-Würfen) als eine stetige und damit auf- und ableitbare Funktion zu beschreiben. Bei der eigentlichen Binomialverteilung als Ergebnis einer Bernoulli-Kette gibt es auf der x-Achse nur stetige Werte, nämlich feste Anzahlen für die Trefferzahl k. Als x-Werte möglich sind nur natürliche Zahlen wie 0, 1, 2, 3 und so weiter. Für k keinen Sinn würde eine echte Kommazahl wie 2,3 machen. Man nennt das auch diskret. Diese Tatsache passt zu dem Fakt, dass der Graph einer Binomialverteilung aus einer Bernoulli-Kette als Säulendiagramm dargestellt wird und nicht als stetige Kurve. Auf ein Säulendiagramm kann man aber nicht den ganzen Apparat der Analysis anwenden. Vor allem kann man nicht auf- und ableiten. Um das zu können, modelliert man oft Säulendiagramme als stetige Funktionen. Für den Fall einer langen Bernoulli-Kette (großes n) berechnet man zunächst σ und μ und setzt sie als Zahlenwert in φ(x) ein. Damit hat man dann eine auf- und ableitbare Funktion, die einigermaßen gut auch lange Bernoulli-Ketten modelliert.
Wahrscheinlichkeiten
Man kann mit der Gaußfunktion keine Wahrscheinlichkeiten für genaue Trefferzahlen k einer Bernoulli-Kette berechnen. Man kann nur Wahrscheinlichkeiten "von-bis" oder "zwischen" berechnen, etwa die Wahrscheinlichkeit für eine Trefferzahl 3≤x≤5. Diese Wahrscheinichkeit entspricht der Fläche unter der Kurve vom linken Rand 3 bis zum rechten Rand 5. Berechnet wird sie über ein Integral.