Exponentielles Wachstum
Definition
Basiswissen
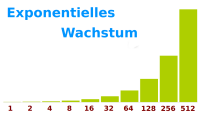
1 ⭢ 2 ⭢ 4 ⭢ 8 ⭢ 16 ⭢ 32 ⭢ 64 - von einem Schritt zum nächsten Schritt rechnet man immer mit derselben Zahl mal. Hier im Beispiel rechnet man: alter Wert mal zwei gibt den nächsten Wert in der Reihenfolge. Ein solches Wachstum nennt man exponentiell. Das ist hier näher erklärt.
Was heißt hier Wachstum?
Wachstum meint hier sehr weit gefasst alles möglichen Dinge. Das Wachstum kann sich etwa auf die Geldmenge beim Sparen beziehen. Das Wachstum könnte auch die Anzahl Elefanten in einem Wildpark meinen. Mehr dazu unter Wachstum ↗
Charakterisierung des exponentiellen Wachstums
Bei einem exponentiellen Wachstum nimmt die betrachtete Größe am Anfang nur sehr langsam zu, die Zunahme wirkt zunächst oft linear. Mit der Zeit wird das Wachstum aber immer stärker, ab einem bestimmten Zeitpunkt kann man es oft als "explosionsartig" bezeichnen. Das trifft zum Beispiel auf die Anzahl von Menschen auf der Erde ab etwa 1900 zu.
Wachstumsschritte
- Mathematisch betrachtet man das Wachstum schrittweise.
- Ein Schritt kann zum Beispiel immer derselbe Zeitraum sein.
- Man könnte dann fragen: wie wächst die Geldmenge in einem Jahr?
- Oder: wie nimmt die Anzahl Elefanten in einem Monat zu?
Exponentiell
- Bei einem exponentiellen Wachstum kommt pro Wachstumsschritt ...
- immer derselbe Anteil der vorherigen Anzahl neu dazu.
- Beispiel: Pro Jahr vermehre sich eine Elefantengruppe so, ...
- dass es am Jahresende die Hälfte mehr Elefanten gibt wie am Jahresanfang.
- In Zahlen könnte das sein: 32 ⭢ 48 ⭢ 72 ⭢ 108 ⭢ 162 ⭢ 243 ...
Konstanter Wachstumsfaktor
- Anstatt zu sagen, dass immer die Hälfte neu dazukommt, ...
- kann man auch sagen, dass der Wachstumsfaktor konstant sei.
- Als Formel: Alte Anzahl mal Wachstumsfaktor = neue Anzahl
- Im Elefantenbeispiel war der Wachstumsfaktor die Zahl 1,5.
- 32 mal 1,5 gab 48.
- 48 mal 1,5 gab 72.
- 72 mal 1,5 gab 108.
- Und so weiter.
x im Exponenten
- Wenn x die Anzahl der Wachstumsschritte meint ...
- und y oder f(x) steht für die Anzahl der wachsenden Dinge ...
- dann kann man Wachstumsvorgänge gut als Exponentialfunktion modellieren:
Formel
- B(x) = a·q^x erweiterte Exponentialfunktion ↗
Legende
- B(x) = Bestand oder Menge zum Zeitpunkt x oder beim x-ten Schritt
- a = Bestand bei x=0, oft der Anfangsbestand, die Startmenge
- q = Wachstumsfaktor oder auch Änderungsfaktor ↗
- x = Anzahl der bisher erfolgten Schritte