Cosinus
Definition
Definition
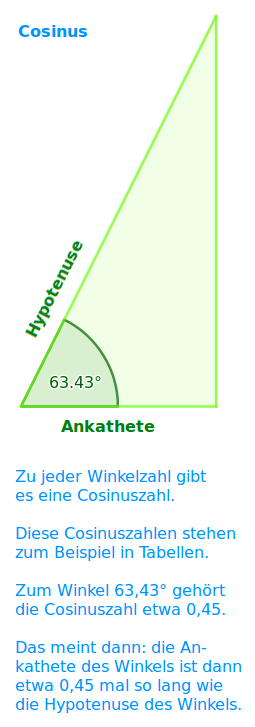
Ankathete durch Hypotenuse: der Cosinus im engeren Sinn gehört immer zu einem festen Winkel in einem rechtwinkligen Dreieck. Zu jeder möglichen Winkelzahl (0 bis 90) gibt es einen dazugehörigen Cosinuswert. Man liest ihn zum Beispiel aus einer Tabelle ab. Der Wert liegt immer zwischen 0 und 1 und sagt, wie viel mal so lang die Ankathete des Winkels ist, wie die Hypotenuse.
Die Formeln vorab
- Cosinus = Ankathetenlänge durch Hypotenusenlänge
- Hypotenusenlänge mal Cosinus gleich Ankathetenlänge
Wofür gilt der Cosinus?
- Der Kosinus im engeren Sinn ist nur für rechtwinklige Dreiecke definiert.
- Eine erweiterte Definition verwendet den Einheitskreis.
- Hier wird nur die Definition am rechtwinkligen Dreieck behandelt.
Definition
- Der Cosinus im engeren Sinn ist nur für rechtwinklige Dreiecke definiert.
- Skizziere ein solches Dreieck gedanklich:
- In dem Dreieck soll es einen 30-Grad-Innenwinkel geben.
- Außerdem gibt es noch einen 60-Grad-Innenwinkel.
- Die Seite gegenüber dem rechten Winkel heißt Hypotenuse.
- Die Hypotenuse ist immer die längste Seite im Dreieck.
- Die zwei Seiten direkt am 90-Grad-Winkel heißen Katheten.
- Für den Cosinus sucht man sich einen der beiden anderen Winkel aus.
- Wir betrachten hier beispielhaft den 30-Grad-Winkel.
- Die Kathete direkt an diesem Winkel ist seine Ankathete.
- Miss nun die Länge der Hypotenuse HY und der Ankathete AK.
- Rechne nun: AK durch HY. Das Ergebnis sollte etwa 0,87 sein.
- Diese Zahl ist der Cosinus von dem 30-Grad Winkel.
- Egal wie ein rechtwinkliges Dreieck aussieht ...
- ein 30-Grad Winkel in ihm wird immer diesen Cosinuswert haben.
Zahlenbeispiel
- Wenn man sagt: der Cosinus von alpha sei 0,3, dann meint das:
- Die Ankathete von alpha hat die 0,3fache Länger der Hypotenuse.
Sonstiges
- "cos 42" zeigt im Lexikon den Cosinuswert von 42 Grad an.
- Die Mehrzahl von Cosinus ist nach Duden "Cosinus" oder "Cosinusse".
- Laut Duden ist auch die Schreibweise "Kosinus" und "Kosinusse" erlaubt.