Brüche subtrahieren
Übersicht
Basiswissen
3/4 minus 1/5 gibt 11/20 - hier sind 4 Methoden beschrieben, wie man das rechnen kann.
Was wird hier erklärt?
- Zum Subtrahieren von Brüchen gibt es verschiedene Verfahren
- Ein Verfahren das immer geht steht unter Bruch minus Bruch ↗
- Die Verfahren hier sind aber oft schneller:
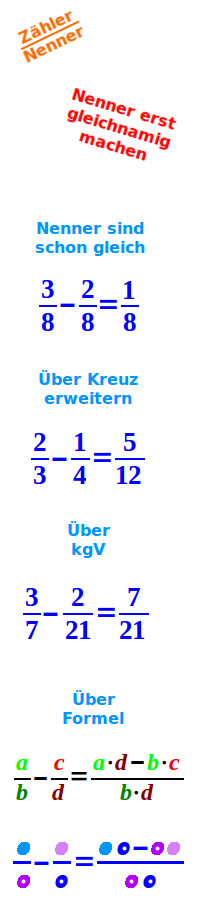
I Nenner sind schon gleich
- Die Nenner sind die Zahlen unten.
- Wenn sie schon gleich sind, ist es einfach.
- Beispiel: 3/8 - 2/8.
- Schreibe ein Gleichzeichen mit ...
- Bruchstrich hinter die Aufgabe.
- Das gibt dann: 3/8 - 2/8 = --
- Schreibe den Nenner (unten) als ...
- neuen Nenner rechts hin.
- Rechne: Zähler links minus Zähler rechts
- Das ist der Zähler vom Ergebnis.
- Das Ergebnis ist also:
- 3/8-2/8=1/8
II Über Kreuz erweitern
- Die Nenner sind noch nicht gleich.
- Beispiel: 2/3 - 1/4
- Hinter die Aufgabe ein Gleichzeichen ...
- mit Bruchstrich schreiben:
- Beispiel: 2/3 - 1/4 = ---
- Jetzt die beiden Nenner (unten) malrechnen.
- 3·4=12; Das ist der neue Nenner.
- Schreibe ihn unter den Bruchstrich rechts.
- Jetzt rechne: oben links mal unten rechts ...
- Also: 2·4·=8. Merke dir das Ergebnis.
- Dann rechne: unten links mal oben rechts.
- Also: 3·1=3. Subtrahiere das von der 8, gibt 5.
- Das ist der neue Zähler (Zahl oben).
- Schreibe diese Zahl oben über den Bruchstrich.
- Ergebnis: 5/12. Fertig.
- Nachteil: oft groß Zahlen
- Vorteil: geht immer
- Siehe auch über Kreuz erweitern ↗
II Über kgV
- Das Standardverfahren aus der Schule
- Beispiel: 2/21 - 3/7
- kgV heißt kleinstes gemeinsames Vielfache.
- kgV von den beiden Nennern (unten) herausfinden.
- Beispiel: 21
- Jetzt überlegen:
- Womit muss man links unten malnehmen, um kgV zu kriegen?
- Beispiel: 21 mal 1 gibt 21, also mit der 1.
- Mit dieser Zahl den ganzen linken Bruch erweitern, gibt: 2/21.
- Womit muss man rechts unten malnehmen, um kgV zu kriegen?
- Beispiel: 7 · 3 gibt 21, also mit der 3.
- Mit dieser Zahl den rechten Bruch erweitern, gibt: 9/21.
- Jetzt haben beiden Brüche einen gemeinsamen Nenner: 21.
- Jetzt rechnen: linker Nenner minus rechten Nenner, gibt 7.
- Das gibt den Zähler (oben) vom Ergebnisbruch.
- Der gemeinsame Nenner (unten) ist auch der Nenner vom Ergebnisbruch.
- Das Endergebnis ist 7/21. Fertig.
- Nachteil: viel Übung nötig
- Vorteil: sehr schnell
IV Über Formel
- Denke dir die Aufgabe als
- a/b-c/d.
- Dann ist das Ergebnis immer:
- (ad-bc)/(bd)
Tipps
- Brüche früh kürzen hält die Zahlen klein
- Das Ergebnis kann man oft noch kürzen.
- 39/30 kann man zu 13/10 kürzen.
- 0/4 ist so viel wie nichts, also 0
- 3/3 ist so viel wie ein Ganzes, also 1