Brüche gleichnamig machen
Methoden
Basiswissen
3/4 und 2/3 gleichnamig gemacht geben 9/12 und 8/12: gleichnamig heißt, dass die Nenner des Bruches (unten) gleich sind. Hier stehen zwei Methoden, wie man das erreichen kann.
Definitionen
- Der Zähler ist die Zahl oben.
- Der Nenner ist die Zahl unten.
- Erweitern meint: Zähler und Nenner mit der gleichen Zahl malrechnen.
- Kürzen meint: Zähler und Nenner durch die gleiche Zahl teilen.
I
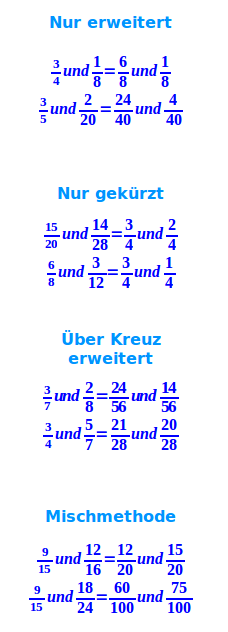
- Nur erweitern ↗
- Man versucht beide Brüche so zu erweitern, dass die Nenner gleich sind.
- Man darf links und rechts mit unterschiedlichen Zahlen erweitern.
- Beispiel: 3/4 und 1/8. Links mit mit 2 erweitern gibt ...
- 6/8 und 1/8. Diese Brüche sind gleichnamig.
- Nachteil: geht nicht immer.
- Vorteil: geht oft leicht.
II
- Nur kürzen ↗
- Man versucht beide Brüche so zu kürzen, dass die Nenner gleich sind.
- Man darf links und rechts mit unterschiedlichen Zahlen kürzen.
- Beispiel: 15/20 und 21/28. Links mit 5 und rechts mit 7 kürzen ...
- 3/4 und 3/4. Das ist die Antwort.
- Vorteil: Geht oft sehr leicht.
- Nachteil: Geht nicht immer.
III
- Über Kreuz erweitern:
- Linken Bruch mit rechtem Nenner erweitern und ...
- Rechten Bruch mit linkem Nenner erweitern.
- Beispiel: 3/7 und 2/8. Links mit 8 und rechts mit 7 erweitern ...
- gibt: 24/56 und 14/56. Das ist die Antwort.
- Nachteil: Zahlen können groß werden.
- Vorteil: geht immer.
IV
- Die Mischmethode:
- Erst kürzen, dann erweitern
- Links und rechts sind unterschiedliche Wege erlaubt.
- Beispiel: 9/15 und 12/16
- Links erst mit 3 kürzen und dann mit 4 erweitern gibt: 12/20
- Rechts erst mit 4 kürzen und dann mit 5 erweitern gibt: 15/20
- Antwort: 9/15 und 12/16 ist wie 12/20 und 15/20.
- Nachteil: mehrere Schritte, viel Probieren.
- Vorteil: geht oft, Zahlen bleiben klein.
Aufgaben dazu
Aufgaben zum gleichnamig-Machen von Brüchen sind hier als Quickcheck zusammengestellt. Zu jeder Aufgabe gibt es auch eine Lösung. Direkt zu den Aufgaben geht es über => qck